轉貼自 自然常數e為什麼這麼重要? - 知乎 (zhihu.com)
為免日後失連,所以在這裡備份一份,並轉為繁體中文。
由於原作是用一般打宇作敍述,沒法表現出數學式,所以這裡用 LaTex 幫忙修訂,但不碓定是否完全正確,所以有錯誤的地方還請不吝指正。
我們知道,自然界有一些十分重要的常數,如 0,1,i,p,e 等,它們的存在很大程度上影響了我們的學習與生活,今天我們就來深度挖掘一下,自然常數 e 為什麼這麼重要?
在回答自然常數 e 為什麼這麼重要之前,我們首先要問,自然常數 e 是什麼? 簡單搜索一下可以發現,百度百科裡面是這麼解釋的:
自然常數,是數學科的一種法則。 約為2.71828,就是公式為 $lim (1+1/x)^x,x→∞$ 或 $lim (1+z)^\frac{1}{z},z→0$,是一個無限不循環小數,是為超越數。
這個解釋給人的感覺就是很高(zhuang)端(bi),對於數學不好的人而言只能用以下反應來形容:
萬萬沒想到,幾個月前,超模君橫空出世,僅用一篇文章,就通俗易懂地闡明瞭 e 的含義,即使是我這種數學殘疾看過去也能一目了然。
這裡以一個銀行存款的例子簡單描述一下:
我們在銀行存款是有利息的,而存款賺到的利息又可以繼續和本金一起,賺取更多的利息。 當然,銀行不是慈善家,它們結算利息的頻率很低,要每一年甚至三年才結算一次,也就是說,在這一年或者三年的時間里,已經獲得的利息並不能幫我們賺取更多利息。
下面考慮一種理想狀況,也就是假定有這樣一家銀行,它一年的存款利率是 100% (簡記為1),並允許我們自由選擇結算利息的次數。 如果我們存入銀行 1 塊錢,那麼我們一年最多能夠賺多少錢呢?
(1) 如果只在年底結算一次利息,由於一年的利率是 1,那麼一年後我們可以連本帶利得到 2 塊錢。
(2) 如果我們要求每半年就結算一次利息,由於半年的利率是 1/2,那麼一年後我們可以連本帶利得到 2.25 塊錢。
(3) 如果我們要求每一個月就結算一次利息,由於一個月的利率是 1/12,那麼一年後我們可以連本帶利得到 2.61 塊錢。(4) 可以看到,利息結算次數越多,年底獲得的收入也就越多。 如果我們腦洞大開,要求銀行時時刻刻為我們結算利息,也就是說結算利息的次數為無數次,那麼我們能否得到無窮無盡的收入,實現數錢數到手抽筋的夢想呢?很遺憾,這個是不可能的! 因為我們最終獲得的收入其實就是下面這個式子,
為什麼 $e^x$ 和 $\ln{x}$ 這麼常見?
然而,即使明白了什麼是自然常數e,作為被高等數學期末考試和研究生考試虐得狼狽不堪的我,還是會冒出以下疑問:
e 不就是增長的極限嗎,你不好好考我求極限,凈考我關於 $e^x$ 和 $\ln{x}$ 的導數積分是什麼意思?重新翻閱以前的資料我才發現,其實這裡涉及到了這兩個函數的特殊性質。
首先是指數函數。 眾所周知,指數函數在我們現實世界中具有重要作用(雖然本人並沒有感覺到),那麼我們便不可避免地需要對指數函數進行求導運算。 指數函數 $y=a^x$ 的導數為
此外,人們為了讓關於 e 的對數函數區別於其它對數函數,甚至還給它另外起了個名字,叫自然對數,並簡單記為 $y=\ln{x}$,這也充分凸顯了自然對數的重要性。
這個時候可能也有人要問了,萬一我要用的就是 $y=2^x$ 或者 $y=\log_2{x}$ 呢? 沒關係,我們可以給它整下容,變成 $y=e^{(x\ln{2})}$ 或者 $y=\log_2{(e\ln{x})}$ (註:原作者在這應該只是示意的表逹,應該用換底公式才對 $y=\ln{x}/\ln{2}$),計算方式並沒有發生本質變化。
通過以上分析,我們可以看到,引入關於 e 的指數函數與對數函數是因為其對應的導數具有極其簡單的形式。 難道歐拉等那些大數學家已經預料到現在的我們考試壓力太大,為了讓我們在考試的時候更容易進行求導計算,大動干戈引入了自然常數e?那麼... 從來沒有感覺到自己這麼重要呢!
哈哈,顯然不是那樣的!
其實,之所以頻繁出現關於 e 的函數,是因為我們現實世界中有太多問題具有以下特點:即一個量的變化與自身大小相關。 而凡是這一類問題,都迫使我們必須引入關於 e 的指數函數或對數函數。
- 理想環境下的種群數量
在生物領域,一個簡單而又經典的問題便是理想環境下的種群數量變化規律。 種群數量越大,種群的增長速率也就越快,種群數量的變化率是和當前種群數量 y 相關的,於是可以簡單描述為
我們已經知道,導數等於自身的函數就是 $y=e^t$。 但是因為右邊存在一個比例常數 λ,所以我們可以假定種群數量 y 隨時間 t 的變化規律符合通用關係 $y=ae^{bt}+c$ (a≠0),從而有- 彈簧振子的運動
※ e 的一些有趣性質
此外,隨著 e 的廣泛應用,人們還發現,e 的性質遠遠不止上述所提及的那麼簡單,它還具有很多其它有趣的性質














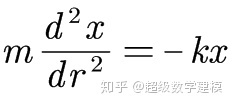





沒有留言:
張貼留言